Елена Удалова

СИММЕТРИИ КУБОВ РАЗНОЙ МЕРНОСТИ
(к вопросу о существовании признаков Рейнина)

Рейнинские признаки типов, разделяющие, подобно юнговским, социон пополам на симметричные группы, не являются независимыми параметрами, а отражают различные свойства как модели А, так и того четырехмерного куба, которым, по сути является социон, состоящий из шестнадцати типов, построенный на Базисе Юнга.

Принятие за основные оси координат юнговских признаков имеет под собой следующие соображения. Во-первых, их выделил в своих наблюдениях сам К.Г. Юнг. Это значит, что они на практике давали наиболее ясную систему независимых (ортогональных) параметров. Во-вторых, именно эти базовые признаки хорошо коррелируют с базовыми свойствами физического мира, в котором пришлось выживать нашим предкам. Информация о веществе (логика), поле (этика), пространстве (сенсорика) и времени (интуиция) — была необходимым и достаточным набором сведений, обеспечивающим успешное выживание в среде обитания.

У других признаков не наблюдается такого ясного соответствия свойствам мира, поэтому мы считаем их дополнительными, хотя, несомненно, из некоторых четверок рейнинских признаков можно построить ортогональный четырехмерный базис. Математика не возражает. Но здесь нам на помощь приходит реальность, потому что соционика, как физика, имеет дело не с умозрительными абстрактными концепциями, а с теми явлениями, которые существуют в окружающем мире.

Вычисления, предпринятые Г.Рейниным, можно назвать скорее теоремой соционики, чем введением новых сущностей.

Но идею наличия дополнительных признаков типов можно продемонстрировать и вполне наглядно, пользуясь несложной геометрией.

Рассмотрим квадрат, являющийся, по сути, двумерным кубом, состоящий из четырех квадратиков (А).

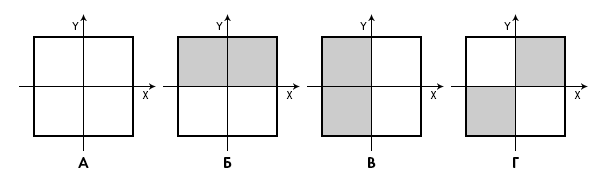
Мы видим, что разделить его пополам на симметричные группы можно тремя разными способами. В нашей соционической реальности такой схеме соответствует, например, деление типов в координатах Логика — Этика (Х) и Интуиция — Сенсорика (Y). По ориентации на вид деятельности.

Тогда вариант Б это группы интуитов (верхние квадратики) и сенсориков (нижние квадратики). Вариант В это деление на группу логиков (левые квадратики) и этиков (правые квадратики). А вариант Г (диагональной симметрии) в этом случае будет состоять из группы интуитологиков + сенсоэтиков (белые квадратики) и группы сенсологиков + интуитоэтиков (серые квадратики). Общим признаком для такого деления будет признак Аристократы (серые квадратики) — Демократы (белые квадратики).

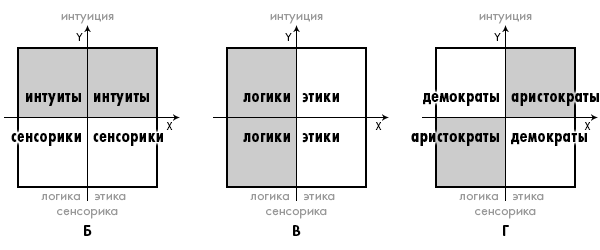
Можно рассмотреть последовательно еще пять сочетаний юнговских признаков по два, отражающие различные свойства групп типов и увидеть, что собой представляют диагональные группы в этих координатах.

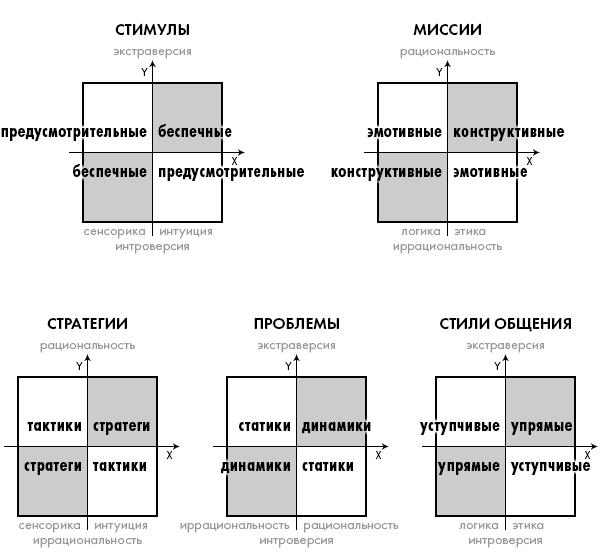
Как видим, это деление социона по некоторым известным нам признакам Рейнина. Т.е. эти признаки выступают как отражение высокой симметрии юнговской классификации. Отметим, что на каждых двух юнговских признаках у нас появился третий, рейнинский. Повторим, что квадрат из четырех элементов можно разбить на симметричные группы тремя способами.

Перейдем теперь к трехмерному, объемному кубу, состоящему из 8 кубиков. Сколькими способами можно его разбить на две симметричные группы? Посмотрим на рисунках.

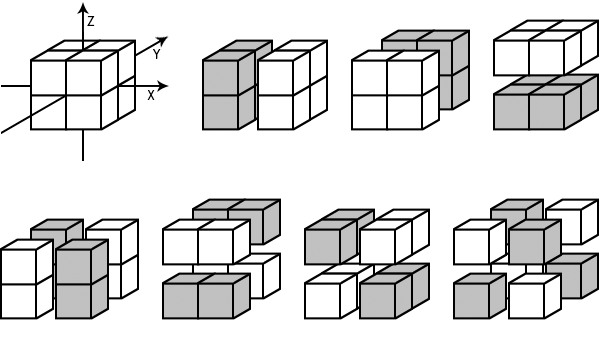
На рисунке отчетливо видно, что куб, состоящий из восьми кубиков, можно разделить пополам на симметричные группы семью различными способами.

Попробуем найти примеры этим признакам в четырехмерном соционическом пространстве.

• Комбинаторика.
  Сочетаниями называют комбинации, составленные из n различных элементов по k, которые отличаются хотя бы одним элементом.
  

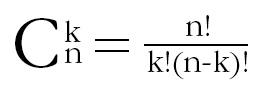
Посмотрим, сколько таких кубиков можно составить из типов социона. Из комбинаторики известно число сочетаний из 4-х по 3. Это 4.

Возможные сочетания		Сочетания конкретных признаков
Комбинация №1	0111	логика/этика, сенс/интуиция, рац/иррац, экстр/интро
Комбинация №2	1011	логика/этика, сенс/интуиция, рац/иррац, экстр/интро
Комбинация №3	1101	логика/этика, сенс/интуиция, рац/иррац, экстр/интро
Комбинация №4	1110	логика/этика, сенс/интуиция, рац/иррац, экстр/интро

Три группы разделений, расположенные параллельно осям координат, соответствуют юнговским признакам, отраженным в значении соответствующей координаты. Нам будут интересны не базисные юнговские признаки, а дополнительные, возникшие из диагональных и шахматной симметрий.

1. В кубе, построенном в координатах сенсорика/интуиция, рациональность/иррациональность и экстраверсия/интроверсия выделим диагональные и шахматную группы.

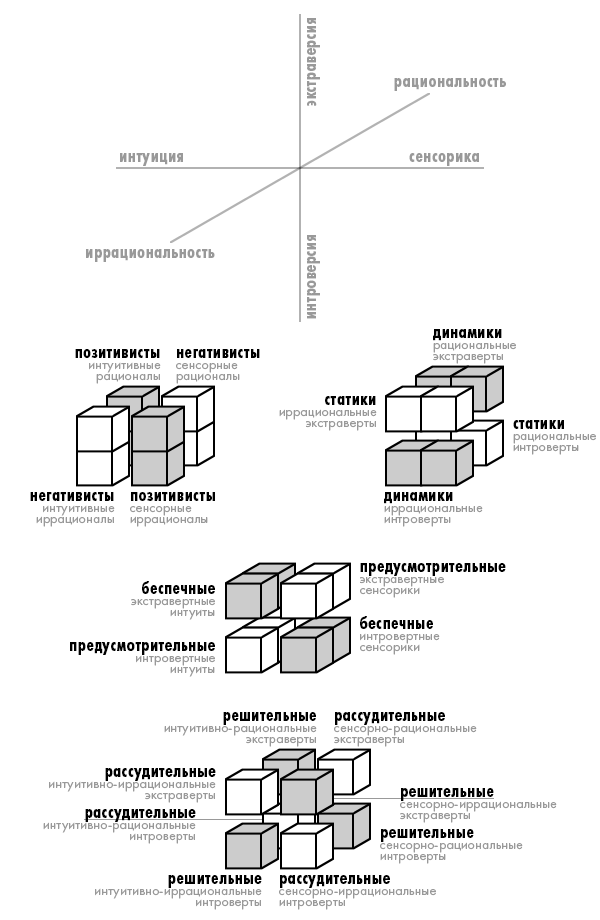
Мы видим, что при таком раскладе диагональные и шахматное деление соответствуют известным нам рейнинским признакам, которые характеризуют группы, полученные симметричным делением фрагментов социона.

2. Возьмем следующий куб, построенный на других координатах: логика/этика, рациональность/иррациональность, экстраверсия/интроверсия. Посмотрим, соответствуют ли рейнинским признакам полученные симметричные группы.

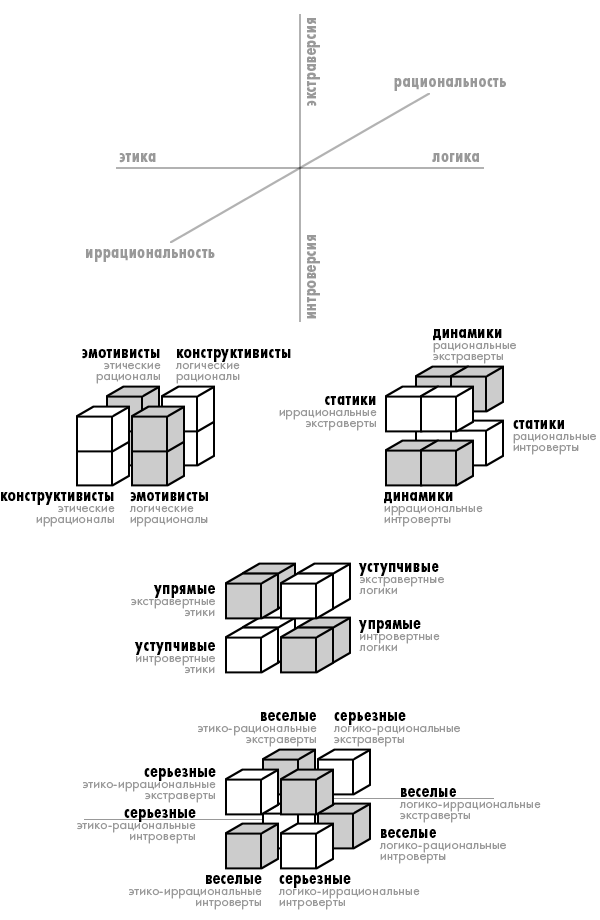
И опять мы видим, что нашим симметричным группам соответствуют известные признаки Рейнина. Некоторые из них повторяются, в соответствии со своими координатами. Некоторые появляются впервые.

3. Третий вариант координатного куба, построенный в соответствии с таблицей возможных сочетаний — это куб с осями логика/этика, сенсорика/интуиция, экстраверсия/интроверсия. Посмотрим, каким рейнинским признакам соответствуют диагональные и шахматное симметричные разделения такого куба.

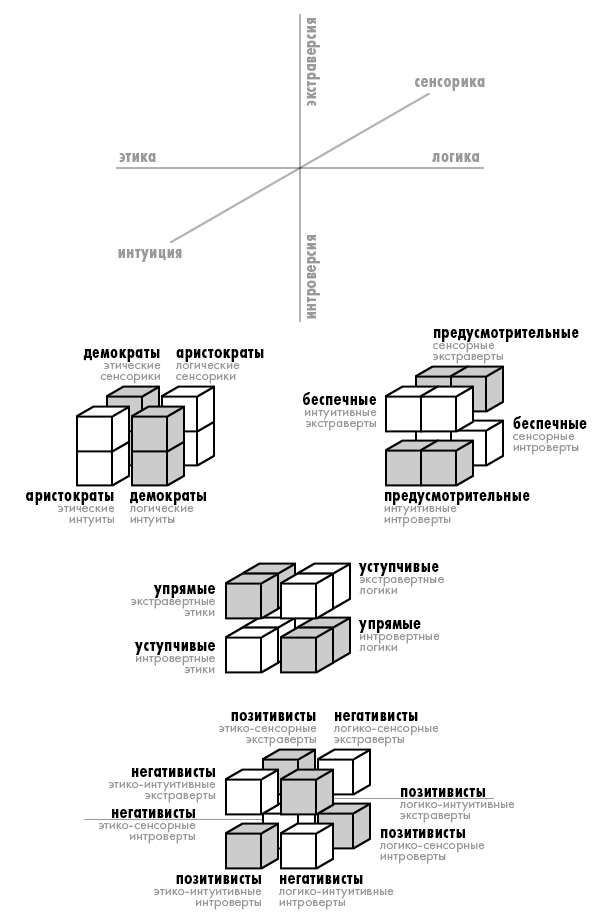
Еще раз убеждаемся, что рейнинские признаки соответствуют симметричным группам, выделенным нами при разбиении кубика.

4. Рассмотрим последний куб, который можно составить на координатах юнговских признаков. Это куб с координатными осями логика/этика, сенсорика/интуиция, рациональность/иррациональность. Посмотрим, каким рейнинским группам соответствуют его симметричные половинки.

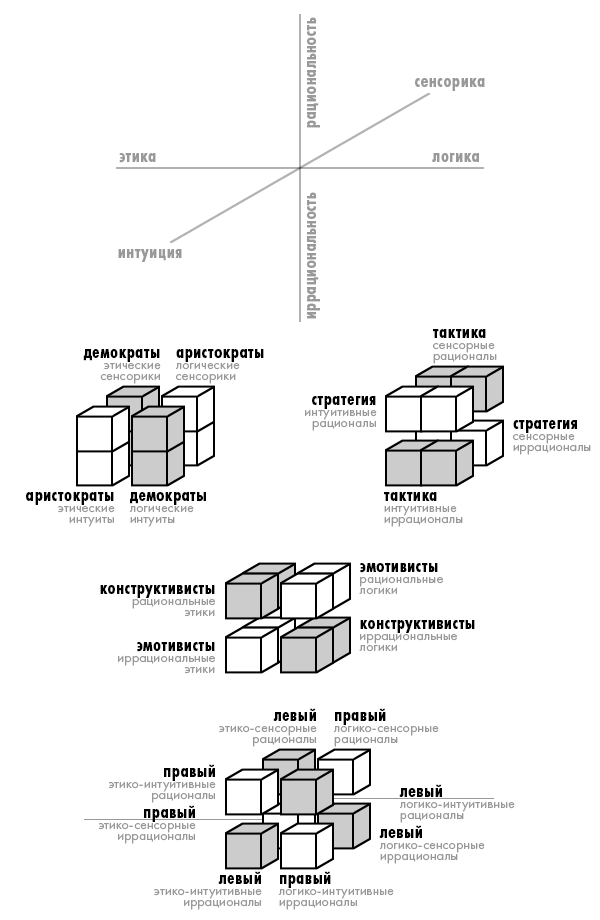
Как видим, эти группы тоже соответствуют рейнинским признакам. При этом, мы исчерпали почти все рейнинские признаки, кроме квестимности/деклатимности.

По сравнению с плоской картинкой, в объемной новые признаки появляются именно в шахматной композиции. Это признаки решительные/рассудительные, веселые/серьезные, позитивисты/негативисты и левые/правые.

Поскольку вообразить себе четырехмерный куб крайне сложно, а изображение его на плоском листе больше похоже на густую паутину, попробуем просто перенести наши наблюдения на куб следующей мерности умозрительно.

Если квадрат из четырех квадратиков мы разбивали на симметричные группы тремя способами, а куб, состоящий из восьми кубиков — семью способами и новые признаки получали только в шахматном разбиении, можно ожидать следующих свойств четырехмерного куба.

Он имеет 16 вершин, т.е. состоит из 16 гиперкубиков.

1. Разбить его на симметричные группы можно пятнадцатью различными способами. Четыре из которых будут юнговскими, соответствующими осям координат. А одиннадцать — дополнительными, соответствующими геометрии разбиения.
2. Вариантов разбиения из 4 по 4 будет всего один.
3. Новый, не отмеченный на предыдущих этапах вариант-признак тоже будет всего один. И соответствовать он будет гипершахматной композиции, которую трудно представить, но несложно описать словами. И это будет признак — квестимность-деклатимность.

В этой гипершахматной композиции будут участвовать типы — по одному на каждый «квадрант» четырехмерного гиперпространства, как и в предыдущих шахматных композициях более низкой мерности.

Деклатимы	Квестимы
Этико-сенсорный рациональный экстраверт Сенсорно-этический иррациональный интроверт Логико-сенсорный рациональный интроверт Сенсорно-логический иррациональный экстраверт Интуитивно-логический иррациональный интроверт Логико-интуитивный рациональный экстраверт Этико-интуитивный рациональный интроверт Интуитивно-этический иррациональный экстраверт	Интуитивно-логический иррациональный экстраверт Логико-интуитивный рациональный интроверт Этико-интуитивный рациональный экстраверт Интуитивно-этический иррациональный интроверт Сенсорно-этический иррациональный экстраверт Этико-сенсорный рациональный интроверт Логико-сенсорный рациональный экстраверт Сенсорно-логический иррациональный интроверт

Резюме

Спорить с математикой о том, что доказанного не существует крайне непродуктивно. Но искать более наглядные объяснения доказанным положениям никогда не лишне. У кого-то это может навести порядок в голове, кто-то откроет новые грани соционической гармонии.

В нашей школе я показываю эти построения на кусочках сахара. К восторгу аудитории ) Возможно, кому-то из коллег этот ракурс тоже поможет сделать сообщение о рейнинских признаках типа более наглядным и доступным.